Reduction / Reformulation of complex process-based models

A data-adaptive approach

As the complexity of a process-based model increases, in most cases the number of adjustable model parameters increases as well. Thus, models of environmental systems typically depend on a large amount of uncertain parameters. As model parameterizations are seldom unique, these models are difficult to handle and often do not provide an insight into the underlying system's effective dynamical modes.
The aim of this study is the re-formulation of model-systems in terms of new easier-to-use state variables that effectively reproduce the complex model's dynamics. We propose a multi-step approach of structural model reduction and reformulation based on the output of a parameter variation of the complex model system.

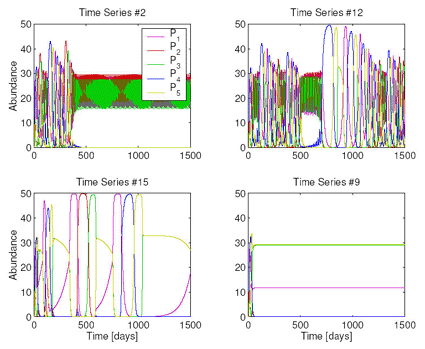
Examples of time series generated by a model of five phytoplankton species competing for three nutrients. Fixed-point, limit cyclc and chaotic dynamics can be seen. 

Methods

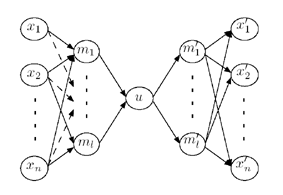
After a possible reduction of the model-generated dataset using unsupervised learning strategies (e.g. Self-Organizing Maps, Growing Neural Gas), the main (structural) reduction is performed by Nonlinear Principal Component Analysis (NLPCA). In this case, an autoassociative neural network was used to extract nonlinear components/modes of the model.

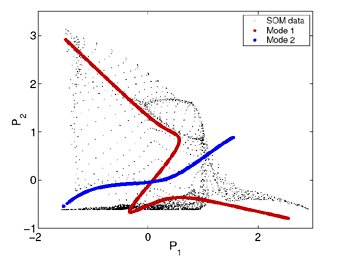
Structure of an autoassociative neural network with hidden nodes (m) and bottleneck-layer (u).	Plot of the first two extracted nonlinear nodes in variable space of the competition model.

These nonlinear modes explain more of the data’s variance than their linear counterparts and seem to be easier to interpret in terms of model variables.

In the last step (which is still in progress), we propose a combination of Genetic Programming (GP), Genetic Algorithm (GA) and nonlinear parameter optimization routines to reformulate a (simple) deterministic model using some of the first nonlinear modes as state variables.
In this framework, systems of differential equations are generated randomly and by recombination of other systems. Model parameters are adjusted using GA to provide starting values for the nonlinear optimization step.

Relevant publications

• Bernhardt, K. and Wirtz, K.W., Reduction of complex models using data-mining and nonlinear projection techniques. In: Pahl-Wostl, C., Schmidt, S., Rizzoli, A.E. and Jakeman, A.J. (eds), Complexity and Integrated Resources Management, Transactions of the 2nd Biennial Meeting of the International Environmental Modelling and Software Society, Volume 1, pp. 57-62. iEMSs, 2004.